Using linear regression with non-linear data
Non Linear Data
Real world data often comes in non-linear relationship. Before we can apply linear regression analysis to such data sets, it is necessary to perform linearity transformation first. Population and economic growths are two examples of exponential functions.
The following table shows a familiar example of compound interest.
| Year | Principal |
|---|---|
| 1 | 10000 |
| 2 | 11000 |
| 3 | 12100 |
| 4 | 13310 |
| 5 | 14641 |
| 6 | 16105.1 |
| 7 | 17715.61 |
| 8 | 19487.171 |
| 9 | 21435.8881 |
| 10 | 23579.47691 |
| 11 | 25937.4246 |
| 12 | 28531.16706 |
| 13 | 31384.28377 |
| 14 | 34522.71214 |
| 15 | 37974.98336 |
| 16 | 41772.48169 |
| 17 | 45949.72986 |
| 18 | 50544.70285 |
| 19 | 55599.17313 |
| 20 | 61159.09045 |
| 21 | 67274.99949 |
| 22 | 74002.49944 |
| 23 | 81402.74939 |
| 24 | 89543.02433 |
| 25 | 98497.32676 |
| 26 | 108347.0594 |
| 27 | 119181.7654 |
| 28 | 131099.9419 |
| 29 | 144209.9361 |
| 30 | 158630.9297 |
It’s easy to see principal growth is exponential.
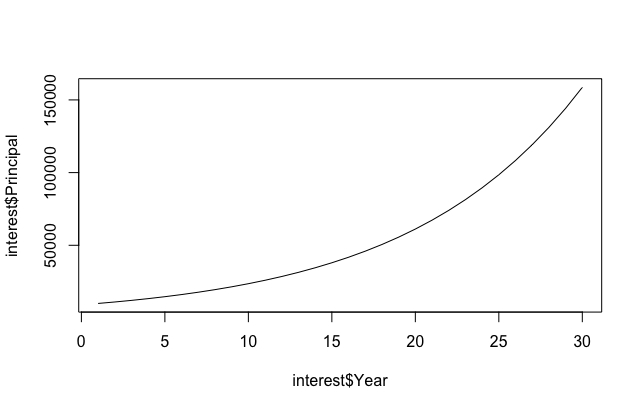
If we attempt to force feed a linear regression model, we’ll get poor results.
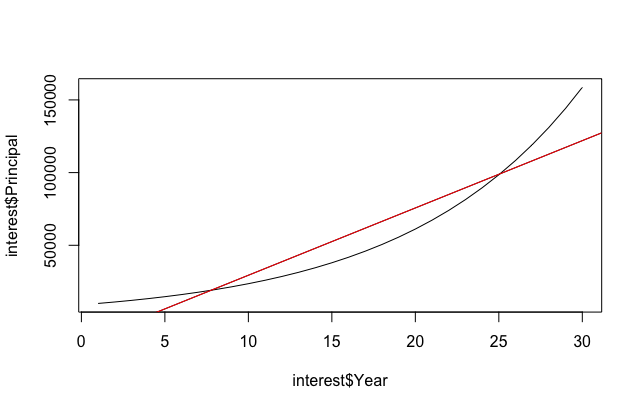
The first step to fix this problem is to understand the nature of the growth of Y with respect to X. Is it a concave function (eg., logarithmic), or is it convex (eg., quadratic, exponential)? In our case, principal growth is exponential, ie., y = ex, so all we need to do is flatten the curve by taking a log.
> interest$LnPrincipal <- sapply(interest$Principal, log)
> interest
Year Principal LnPrincipal
1 1 10000.00 9.210340
2 2 11000.00 9.305651
3 3 12100.00 9.400961
4 4 13310.00 9.496271
5 5 14641.00 9.591581
6 6 16105.10 9.686891
7 7 17715.61 9.782201
8 8 19487.17 9.877512
9 9 21435.89 9.972822
10 10 23579.48 10.068132
11 11 25937.42 10.163442
12 12 28531.17 10.258752
13 13 31384.28 10.354063
14 14 34522.71 10.449373
15 15 37974.98 10.544683
16 16 41772.48 10.639993
17 17 45949.73 10.735303
18 18 50544.70 10.830613
19 19 55599.17 10.925924
20 20 61159.09 11.021234
21 21 67275.00 11.116544
22 22 74002.50 11.211854
23 23 81402.75 11.307164
24 24 89543.02 11.402475
25 25 98497.33 11.497785
26 26 108347.06 11.593095
27 27 119181.77 11.688405
28 28 131099.94 11.783715
29 29 144209.94 11.879025
30 30 158630.93 11.974336
> plot(interest$Year, interest$LnPrincipal, type='l')We can verify that ln(Principal) is indeed linear.
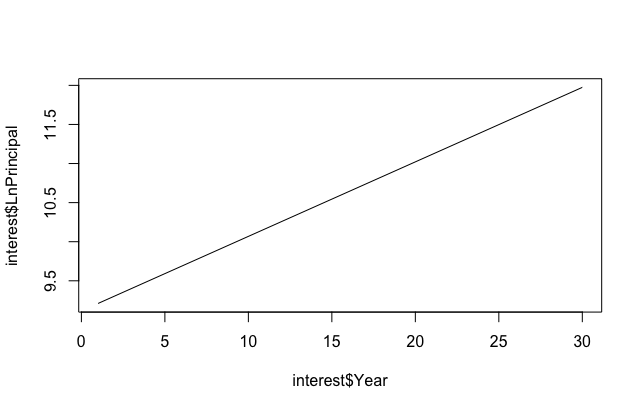
We then run linear regression on ln(Principal). To find out the log values of the principals, we use the predict function.
> reg <- lm(LnPrincipal ~ Year, data=interest)
> predicted <- data.frame(Year=1:35)
> predicted$LnPrincipal <- predict(reg, newdata=predicted)
> predicted
Year LnPrincipal
1 1 9.210340
2 2 9.305651
3 3 9.400961
4 4 9.496271
5 5 9.591581
6 6 9.686891
7 7 9.782201
8 8 9.877512
9 9 9.972822
10 10 10.068132
11 11 10.163442
12 12 10.258752
13 13 10.354063
14 14 10.449373
15 15 10.544683
16 16 10.639993
17 17 10.735303
18 18 10.830613
19 19 10.925924
20 20 11.021234
21 21 11.116544
22 22 11.211854
23 23 11.307164
24 24 11.402475
25 25 11.497785
26 26 11.593095
27 27 11.688405
28 28 11.783715
29 29 11.879025
30 30 11.974336
31 31 12.069646
32 32 12.164956
33 33 12.260266
34 34 12.355576
35 35 12.450886
> So far, what we’ve got is the log values of principals. To get the actual dollar values, we only have to raise e to the log values.
> predicted$Principal <- sapply(predicted$LnPrincipal, exp)
> predicted
Year LnPrincipal Principal
1 1 9.210340 10000.00
2 2 9.305651 11000.00
3 3 9.400961 12100.00
4 4 9.496271 13310.00
5 5 9.591581 14641.00
6 6 9.686891 16105.10
7 7 9.782201 17715.61
8 8 9.877512 19487.17
9 9 9.972822 21435.89
10 10 10.068132 23579.48
11 11 10.163442 25937.42
12 12 10.258752 28531.17
13 13 10.354063 31384.28
14 14 10.449373 34522.71
15 15 10.544683 37974.98
16 16 10.639993 41772.48
17 17 10.735303 45949.73
18 18 10.830613 50544.70
19 19 10.925924 55599.17
20 20 11.021234 61159.09
21 21 11.116544 67275.00
22 22 11.211854 74002.50
23 23 11.307164 81402.75
24 24 11.402475 89543.02
25 25 11.497785 98497.33
26 26 11.593095 108347.06
27 27 11.688405 119181.77
28 28 11.783715 131099.94
29 29 11.879025 144209.94
30 30 11.974336 158630.93
31 31 12.069646 174494.02
32 32 12.164956 191943.42
33 33 12.260266 211137.77
34 34 12.355576 232251.54
35 35 12.450886 255476.70
> As we can see, the predicted values fit the observed ones remarkably well.