After running linear regression, it’s important to check for residual. The residual of a linear regression model is the difference between the observed value of the dependent variable y and the fitted value ŷ.

The following table shows how energy bar sales correlate with price and marketing expenditure.

Store Sales Price Advertising
1 4141 59 200
2 3842 59 200
3 3056 59 200
4 3519 59 200
5 4226 59 400
6 4630 59 400
7 3507 59 400
8 3754 59 400
9 5000 59 600
10 5120 59 600
11 4011 59 600
12 5015 59 600
13 1916 79 200
14 675 79 200
15 3636 79 200
16 3224 79 200
17 2295 79 400
18 2730 79 400
19 2618 79 400
20 4421 79 400
21 4113 79 600
22 3746 79 600
23 3532 79 600
24 3825 79 600
25 1096 99 200
26 761 99 200
27 2088 99 200
28 820 99 200
29 2114 99 400
30 1882 99 400
31 2159 99 400
32 1602 99 400
33 3354 99 600
34 2927 99 600

We then build a linear regression model, reg.

> sales <- read.csv("energy_bar.csv")
> reg <- lm(sales$Sales ~ sales$Price + sales$Advertising)

To plot reg’s residual:

> res <- resid(reg)
> plot(sales$Sales, res)
> abline(0,0)
>

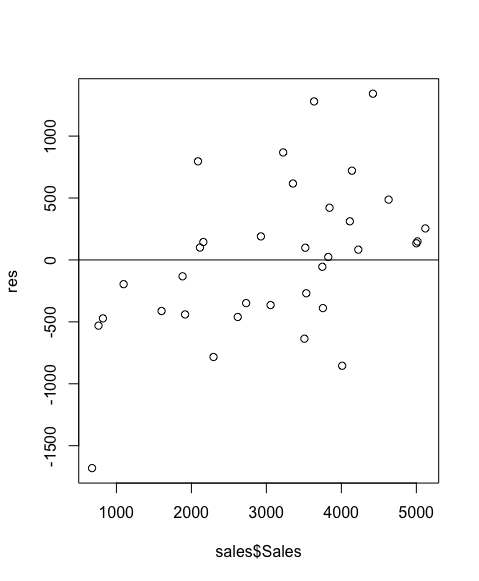
residual

Recall that in linear regression, we’re fitting a straight line to observed values. Some observed values will be underestimated (y > ŷ); some overestimated (y < ŷ); and others right smack on the line (y = ŷ). If the fitted line is a good estimator, then the under- and over-estimations should be random and cancel out each other, on average. This is what is shown in the residual plot above, showing the residual values dancing around the zero line.

Any pattern on the residual plot indicates a systemic error in the model. It could be outliers. Sometimes, data may need to be manually cleaned up. Alternatively, the data set may not in fact be linear. In which case, linearity transformation may be required to flatten a concave or convex function. But the main point is that residual patterns always require investigation.